W kartezjańskim układzie współrzędnych na płaszczyźnie narysowano kwadrat o boku długości 400 i środku symetrii w punkcie (200;200). Boki kwadratu są równoległe do osi układu współrzędnych. W kwadrat wpisano koło. Następnie wylosowano 10 000 punktów należących do kwadratu. Współrzędne (x,y) punktów zostały zapisane w pliku "punkty.txt", każdy punkt w osobnym wierszu. Wiersz ma postać dwóch liczb całkowitych z zakresu <0;400>, rozdzielonych pojedynczym znakiem odstępu.

Zadanie 4.1. (0–3)
Wypisz współrzędne tych punktów, które należą do brzegu koła (okręgu), oraz podaj liczbę punktów należących do wnętrza koła (brzeg koła nie należy do wnętrza koła).
Wskazówka:
Równanie okręgu o środku w pkt S=(a,b) i r> 0
(x-a)² + (y-b)² = r²
Dla pliku danych wśród pierwszych 100 punktów 80 należy do wnętrza koła.
Odp:
Punkty okręgu: (256,8) (200,400).
Liczba punktów leżących wewnątrz koła: 7852.

Zadanie 4.2. (0–3)
Przy założeniu równomiernego rozkładu punktów w kwadracie, stosunek liczby punktów n_k należących do koła do liczby punktów n należących do kwadratu jest w przybliżeniu równy stosunkowi pola koła P_k do pola kwadratu P:
n_k/n ≈ P_k/P
Dla przypomnienia:
P_k = π r²
Wyznacz przybliżoną wartość liczby pi, biorąc pod uwagę punkty z pliku punkty.txt:

pierwszych 1000 punktów,

pierwszych 5000 punktów,

wszystkie punkty.
Wyniki zaokrąglij do 4 miejsc po przecinku.
Informacja:
Przybliżona wartość liczby pi dla pierwszych 100 punktów z pliku wynosi 3,2000.
Odp:
a) 3,2280 albo 3,228
b) 3,1656
c) 3,1416

Zadanie 4.3. (0–5)
Błąd bezwzględny przybliżonej wartości liczby pi, wyznaczonej z n punktów, definiujemy następująco:
ε_n=|π-pi_n|
gdzie:
π - wartość liczby pi, będąca wynikiem standardowej funkcji z narzędzia informatycznego, z którego korzystasz;
pi_n - przybliżona wartość liczby pi wyznaczona z n kolejnych punktów, poczynając od pierwszego punktu z pliku punkty.txt, np. pi₁₀₀₀ – liczba wyznaczona z pierwszego tysiąca punktów.

Oblicz ε_n dla n = 1, 2, 3, …, 1700. Na podstawie powyższego zestawienia utwórz wykres liniowy ilustrujący zmiany dokładności wyznaczanej liczby pi. Zadbaj o czytelność wykresu. Wartości dla ε₁₀₀₀ oraz ε₁₇₀₀ (zaokrąglone do czterech miejsc po przecinku) zapisz do pliku.
Odp:
ε₁₀₀₀ = 0,0864; ε₁₇₀₀ = 0,0184

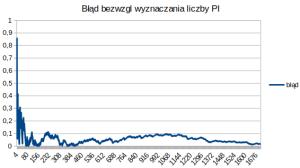
(Konieczny opis wykresu)