Naukowcy śledzą zmiany pogody na odległej planecie. Chmury występujące na niebie tej planety podzielono na dwie kategorie, nazwane przez analogię do ziemskich cirrusami (C) i stratusami (S). W każdej z kategorii chmury są klasyfikowane względem wielkości od 1 do 5. Mamy zatem chmury dziesięciu rodzajów: C1, C2, C3, C4 i C5 oraz S1, S2, S3, S4 i S5. Na tej planecie w jednym dniu mogą występować chmury tylko jednego rodzaju.
W każdym z 500 kolejnych dni stacja badawcza umiejscowiona na planecie mierzyła temperaturę w stopniach oraz określała rodzaj chmur. Dane te zawarte są w kolejnych wierszach pliku pogoda.txt. Każdy wiersz pliku pogoda.txt zawiera kolejno:

numer dnia (od 1 do 500),

zmierzoną temperaturę (z dokładnością do jednego miejsca po przecinku, temperatura nigdy nie spada poniżej zera),

wielkość opadu, jaki miał miejsce tego dnia (w milimetrach, zaokrąglony do liczby całkowitej),

kategorię chmur (C, S lub 0 – jeśli dzień był bezchmurny),

wielkość chmur (od 1 do 5 lub 0 – jeśli dzień był bezchmurny).

Dane oddzielone są średnikami, pierwszy wiersz jest wierszem nagłówkowym.
Przykład:
Dzien;Temperatura;Opad;Kategoria_chmur;Wielkosc_chmur
1;19;0;0;0
2;22;1;C;1
3;23,6;4;C;1
W dniu 301. kamera na stacji badawczej się zepsuła i od tego dnia stacja raportowała wszystkie dni jako „bezchmurne”, temperatura i opady jednak dalej były poprawnie mierzone.

Zadanie 5.1. (0–2)
Podaj liczbę dni o temperaturze większej lub równej 20 stopni i jednocześnie o opadzie mniejszym lub równym 5 mm.
odp: 63

Zadanie 5.2. (0–2)
Znajdź najdłuższy ciąg kolejnych dni, w których temperatura zmierzona każdego dnia jest wyższa niż temperatura dnia poprzedniego. Jest tylko jeden taki ciąg. Podaj numer pierwszego i numer ostatniego dnia w takim ciągu.
Na przykład dla danych:
dzień temperatura
34 3,7
35 3,4
36 3,5
37 3,6
38 3,7
39 3,5

pierwszym dniem ciągu spełniającym warunek zadania jest dzień 36, a ostatnim – 38.
odp: 448-455

Zadanie 5.3. (0–3)
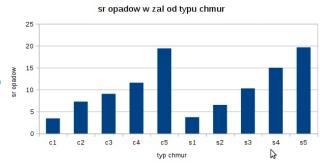
Dla pierwszych 300 dni pomiaru oblicz, z dokładnością do dwóch miejsc po przecinku, średni opad dla każdego rodzaju chmur (kategoria + wielkość, czyli C1, C2, C3, C4, C5, S1, S2, S3, S4, S5). Przedstaw wyniki na wykresie kolumnowym, pamiętając o czytelnym opisie wykresu.
odp:
C1 3,45
C2 7,28
C3 9,05
C4 11,58
C5 19,4
S1 3,73
S2 6,52
S3 10,29
S4 15
S5 19,64


Zadanie 5.4. (0–4)
Profesor George Nubis przedstawił teorię, według której chmury określonej wielkości i kategorii rozwijają się w następujący sposób:

jeśli w danym dniu nie ma chmur, nazajutrz na pewno pojawią się chmury o wielkości 1,

chmury po trzech dniach samoczynnie przechodzą w chmury o wyższym numerze, aż do numeru 5,

chmury o wielkości 5 zanikają wtedy, gdy spadnie w ciągu dnia co najmniej 20 mm deszczu, a wówczas następny dzień jest bezchmurny,

powstanie chmur kategorii C lub S zależy od temperatury powietrza w dniu ich tworzenia się. Jeśli temperatura w dniu pojawienia się chmur jest nie mniejsza niż 10 stopni, to powstają chmury kategorii C (o wielkości 1), w przeciwnym wypadku – chmury kategorii S (o wielkości 1).

Uwaga: Przez pierwszych 20 dni teoria zgodziła się dokładnie z obserwacjami. Użyj tej informacji, aby sprawdzić swoje obliczenia.
Załóż, że chmury rozwijałyby się przez cały czas (500 dni) według teorii profesora i że dzień pierwszy był bezchmurny (wielkość chmur 0), a następnie:
a) podaj liczbę dni (spośród wszystkich 500) z chmurami wielkości 0, 1, 2, 3, 4 i 5 – dla każdej wielkości oddzielnie (przyjmij, że wielkość opadu w danym dniu jest taka, jaką zapisano w pliku z danymi),
b) dla pierwszych 300 dni pomiaru podaj, ile wśród nich było takich, w których teorię profesora Nubisa dotyczącą wielkości chmur potwierdzały odczyty z kamery,
c) dla pierwszych 300 dni pomiaru podaj, ile wśród nich było takich, w których teorię profesora Nubisa dotyczącą kategorii chmur potwierdzały odczyty z kamery.
odp:
0 34
1 102
2 102
3 102
4 100
5 60

296

286